Overview
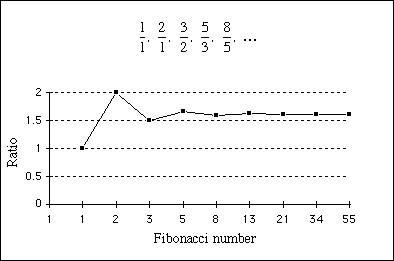
The Golden Ratio (aka the Golden Section, the Golden Mean, the Divine Proportion, etc.) is defined by the relationship of smaller entity A and larger entity B such that the ratio of A:B is the same as that of B:A + B. This ratio is a constant and is roughly equal to 0.618, or phi (ϕ). Interestingly, dividing B/A and A+B/B yields a constant with the same numeric sequence after the decimal: 1.618… This number is called Phi (Φ). The Golden Ratio is closely tied to the Fibonacci sequence, wherein each number is the sum of the two numbers that precede it (1,1,2,3,5,8,13,21,34, 55...). Dividing each number by its successor yields quotients that converge towards phi (1, 0.5, 0.666, 0.625, 0.615, 0.619, 0.617, 0.618...).
The first recorded reference to what we now call the Golden Ratio is in Euclid's Elements (ca. 300 BCE), in which the Greek mathematician describes "the extreme and mean ratio."

Renaissance humanists revived interest in this ratio, which they called the "divine proportion." In his De Divina Proportione (1509), Luca Pacioli explains why this ratio deserves the sacred moniker. He equates the mystery of God to the mystery of this irrational number, and adds that the three lengths that make up the definition of the Divine Proportion echo the three parts of the Trinity.

The Golden Ratio has captivated scholars of all disciplines -- from botany to art history -- for centuries, and frequently pops up in popular culture today.
Click on the other tabs to learn about the Golden Ratio's role in art and nature, and to explore its possible presence in ten works of art.