The Golden Ratio in Nature
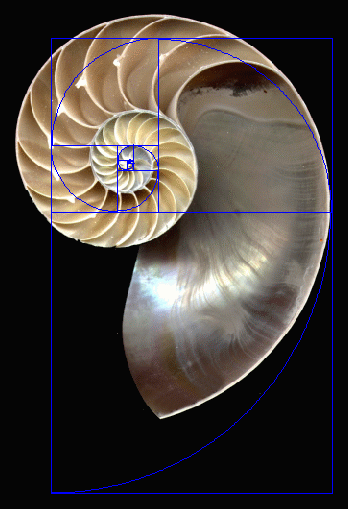
The nautilus shell is perhaps the most famous example of the Golden Ratio, or more specifically the Fibonacci sequence, appearing in nature. As Gary Meisner points out, however, the shell's spiral does not fit a "traditional" golden ratio spiral, which is based on 90-degree turns (A), but a 180-degree golden ratio spiral (B). In the popular imagination, Image A is much more prevalent.
A B

Many flowers have numbers of petals that correspond to Fibonacci numbers; for example, a clematis has 8, a marigold 13, a shasta daisy 21, and a sunflower 34.



shasta daisy = 21 clematis = 8 sunflower = 34
One can also associate the sunflower with the Golden Ratio in another way. Its center consists of a series of interlocking curves running in opposite directions. The total number of each of the two types is always a Fibonacci number. Most sunflowers contain 55 long curves and 89 short curves; for some the ratio is 89 to 144. This Fibonacci-based arrangement constitutes an extremely efficient growth pattern.
